230201 1L2L0X0B_(I), http://farbe.li.tu-berlin.de/BGRI.HTM oder http://color.li.tu-berlin.de/BGRI.HTM

Für diese Hauptseite mit Text und besonderen Bildern
der zugehörigen Bildseite mit 10 Farbserien, siehe BERI in englisch, BGRI in deutsch.
Für die vorherige Hauptseite, siehe BEQI in englisch, BGQI in deutsch.
Für die nächste Hauptseite, siehe BESI in englisch, BGSI in deutsch.

Für Links zum Kapitel B Farbensehen und Farbmetrik (2020), siehe
Inhaltsliste von Kapitel B: BEA_I in englisch oder BGA_I in deutsch.
Zusammenfassung von Kapitel B: BEA_S in englisch oder BGA_S in deutsch.
Beispielbildteil von 26 Teilen BGAS bis BGZS: BEAS in englisch oder BGAS in deutsch.

Kapitel B: Farbensehen und Farbmetrik (2020), Hauptteil BGRI

1. Einführung und Ziele

Die Ostwald-Farben haben die maximalsten Buntwerte CAB2 von allen Körperfarben. Die Wellenlängenbereiche der Ostwald-Farben werden durch kompensative Wellenlängen begrenzt. Sie bilden daher ein "Farbenhalb". Die Wellenlängengrenzen ändern sich etwas mit der Lichtart.


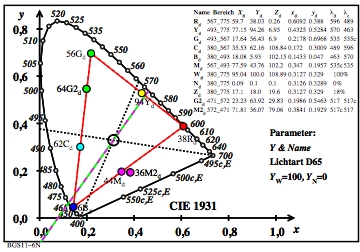
Bild 1 zeigt die Ostwald-Optimalfarben in der Normfarbtafel (x, y) für die Farbpaare R-C, Y-B und G-M.
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe BGS11-6N.PDF.

Das Farbpaar G-M hat die Wellenlängengrenzen 493 nm und 567 nm. Die Farben G und M sind Optimalfarben, aber keine Ostwald-Optimalfarben.

Jedoch das Farbenhalbpaar G2-M2 ist eine Ostwald-Optimalfarbe. Die Farben G2 und M2 haben in Bild 1 die Wellenlängengrenzen 471 nm und 572 nm. Die beiden zugehörigen Farbenhalbs mit diesen Wellenlängengrenzen sind durch eine Gerade in den Farben Grün und Magenta definiert.

2. Gerade erkennbare Farbunterchiede (JNDs) von Ostwald-Farben

Die Ostwald-Farben entstehen durch spektrale Farbmischung mit einem Farbintegrator. Durch Masken werden nur bestimmte weiße Bereiche in Bild 2 gemischt.


Bild 2: Spektrale Mischung der Ostwald-Optimalfarben mit Masken zu einer homogenen Farbe mit einem spektralen Farbintegrator
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe BGR10-7N.PDF.

Ein Zweistrahl-Farbintegrator erlaubte die Farberzeugung von zwei gleichen Ostwald-Optimalfarben in zwei kreisförmigen Halbfelden. Eine der beiden Masken wurde so lange verschoben, bis zu 50% ein gerade erkennbarer Unterschied (JND) erkennbar war. Das Experiment wurde anschliessend mit der negativen Maske wiederholt. Zu den beiden Masken gehörten immer komplementäre Optimalfarben. Die Verschiebung der beiden Masken war für diese beiden komplementären Optimalfarben immer annähernt gleich. Dies wird durch gleiche Verschiebung der Masken nach rechts und links gezeigt. Die Verschiebung ist für beide Farben G2 und M2 gleich.

3. Gleiche JNDs für alle antagonistischen (komplementären) Optimalfarben nach Holtsmark und Valberg

Das experimentelle Ergebnis hat besondere Bedeutung für die Farbmetrik:

a. Das Experiment benutzt zwei aneinandergrenzende Farben im weißen Umfeld und im Dunkelraum. Das logarithmische Mittel der Hellbezugswerte von Weiß und Schwarz kann ein mittelgraues Gesichtsfeld mit Yu definieren.

b. Nach CIE 230:2019 gilt hier weitgehend das Gesetz von Weber-Fechner in der folgenden Form:

L* = k log[Rn] (k = 1 oder 0,86, Rn=R/0,20 normierte Reflexion) [1]

dann gilt für die Ableitung

d(L*) = k d(Rn)/Rn [2]

Für gleiche visuelle Unterschiede d(L*)=1 gilt:

Rn / d(Rn) = k [3]

Anstelle der normierten Reflexion Rn wird in der Farbmetrik auch der normierte Hellbezugswert Yn = Y/Yu oder die normierte Leuchtdichte Ln=L/Lu benutzt. Für das graue Umfeld ist Yu der Hellbezugswert und Lu die Leuchtdichte. Der Quotient nach Gleichung [3] ist unabhängig von der Normierung.

In der Regel gilt für den Hellbezugswert des grauen Umfeldes

log Yu = 0,5 (log[YN] + log [YW]) [4]

Bei Körperfarben ist im Idealfall YW=100 für Weiß W und YN=4 für Schwarz N. Der Wert YN=4 gilt angenähert für alle matten schwarzen Köperfarben. Dann ist der Hellbezugswert nach Gleichung [4]:

Yu = 20 [5]

Der Wert nach Gleichung [5] wird zum Beispiel in den Farberscheinungsmodellen CIECAM02 und CIECAM16 (2021 in CIE-Abstimmung) benutzt.

Es ist von besonderer Bedeutung, dass Gleichung [1] für verschiedene Konstanten k mit der folgenden Form äquivalent ist:

L* = c log [Rn^m] [6]

Die Variable L* wird nach Stiles als das Linienelement zur Variablendifferenz dL* bezeichnet.

Für gerade erkennbare Unterschiede (JNDs) auf grauer Umgebung gilt für

- aneinandergrenzende Farben: m=1 (oder 0,86)

- separate Farben: m=0,5 (oder 0,43=0,86/2=1/2,4).

Der Wert 2,4 wird als Gammawert in der Informationstechnik angewendet. Im sRGB-Farbenraum nach IEC 61966-2-1 approximiert der Gammawert die CIELAB-Helligkeit. Es gilt angenähert L*CIELAB = L*IECsRGB mit

L*CIELAB = 116 (Y/100)^(1/3) - 16 [7]

und

L*IECsRGB = 100 (Y/100)^(1/2,4) [8]

Zusammenfassung:
Zum Beispiel zur Beschreibung der Farbunterschiede von aneinandergrenzenden und separaten Farben auf grauer Umgebung, kann daher das Linienelement in Gleichung [1] oder das Weber-Fechner-Verhältnis [2] mit verschiedenen Konstanten m angewendet werden.

Die S-förmige Signalfunktion der Farbphysiologie wird durch eine antagonistische logarithmische Funktion um das graue Umfeld (Ru=0,2 oder Yu=20) erreicht. Diese Funktion hat den Wert 0 für das graue Umfeld.

4. Bunttonkreise und Bunttonebenen von Ostwald-Farben für 8 CIE-Lichtarten und 2 Kontraste C>288:1 und 2:1

Anstelle der normierten Reflexion Rn oder dem normierten Hellbezugswert Yn werden für bunte Farben auch die linearen Buntwerte CAB2 betrachtet. Für ihre Berechnung siehe die Gleichungen und Tabellen in den Bildern.


Bild 3: Ostwald-Optimalfarben im Buntdiagramm (A2, B2) für die drei Farbpaare R-C, Y-B und G-M
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe BGR31-7N.PDF.

Parameter sind der Helbezugswert Y mit Farbname, zum Beispiel 94Yd oder 6Bd für das Farbpaar Y-B. Die Hellbezugswerte betragen Y=94 für Gelb Yd und Y=6 für Blau Bd. Die Hellbezugswerte unterscheiden sich daher um einen Faktor 15.

Die Buntwerte CAB2 sind für alle Farbpaare und die 8 Lichtarten innenhalb von 10 Prozent gleich. Die Lichtarten enthalten die CIE Normlichtarten D65 und A. Der gleiche Buntwert CAB2 ist ein besonderer Vorteil für viele Anwendungen.


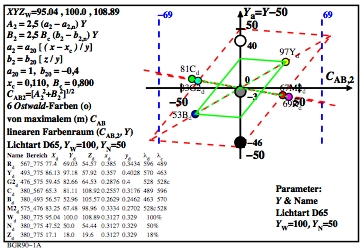
Bild 4: Ostwald-Optimalfarben in der Bunttonebene Y-B
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe BGR90-1A.PDF.

Die Hellbezugswerte von Gelb und Blau sind um den Faktor 15 verschieden. Die Buntwerte CAB2 sind nahezu gleich groß. Als Ordinate dient die lineare Hellbezugswertdifferenz Y-50.

In späteren Bildern ist die Ordinate das empfindungsgemäße Farbmerkmal L*, vergleiche Gleichung [6] mit den normierten Werten Yn = Y/20.

L* = log [Yn^k]

Für graue Umgebung ist der Exponent k für separate Farben oft nur halb so groß wie für aneinandergrenzende Farben.


Bild 5: Ostwald-Optimalfarben in der Bunttonebene R-C.
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe BGR91-1A.PDF.

Die Hellbezugswerte Y von Rot und Cyan betragen 81 und 69. Die Buntwerte CAB2 sind nahezu gleich groß. Als Ordinate dient die lineare Hellbezugswertdifferenz Y-50.

Die grünen Kurven in Bild 4 und 5 gelten für den Kontrast C=2:1. Die schwarzen Kurven gelten für den theoretischen Szenenkontrast C>=288:1. Der visuelle Kontrast Cvis = Y / dY ist oft nur C=25:1 für aneinandergrenzende Farbfelder mit Y nahe dem Umfeld.

5. Zusammenhang der Holtsmark-Ergebnisse mit farbmetrischen Linienelementen von Schroedinger und Stiles

Nach Holtsmark und Valberg haben alle komplementären Optimalfarben angenähert gleiche JNDs.

Für komplementäre Optimalfarben sind die Farbreizdifferenzen deltaX, deltaY und detaZ zur Erzeugung einer gerade erkennbaren Differenz (JND) gleich. Dies gilt auch für alle linearen Transformationen, zum Beispiel die Buntwerte deltaA2, deltaA3 und den Hellbezugswert deltaY.

Daher kann das folgende Farblinienelement von E. Schroedinger, das von W.S Stiles beschrieben und interpretiert wurde, fortentwickelt werden:

ds^2 = 1/(lr R + lg G + lb B) [dR^2/R + dG^2/G + dB^2/B] [9]

In dieser Gleichung sind die Konstanten lr, lg und lb die Leuchtdichtebeiwerte. Die Unterscheidung in Helligkeitsrichtung ist die gleiche für alle Farben. Es gibt keine Kreuzterme, zum Beispiel zwischen R und G. Kreuzterme sind zur Erzeugung der Eigenschaft Additivität der kleinstufigen Helligkeit nicht erlaubt.

Die Additivitätseigenschaft scheint auch im sRGB-Farbenraum nach IEC 61966-2-1 enthalten zu sein. Die Farbwerte rgb* sind proportional zu den Gerätefarbwerten RGBd (d=device) gestuft. In Helligkeitsrichtung sind alle drei Farbwerte rgb* proportional zu L*CIELAB zur Codierung und Übertragung gestuft. Die sRGB-Farbwerte rgb* sind deshalb mit einem Stern (*) gekennzeichnet.

Werden die drei Richtungen RGB im Linienelement von Schroedinger durch die drei antagonistischen Paare R-C, Y-B, und G-M ersetzt, so bleibt der Farbenraum weiterhin dreidimensional. Zum Beispiel vom dem Farbpaar R-C ist jeweils eine Komponente größer und diese bestimmt die Bunttonebene.

Schroedinger hat das Eigenlicht Ro, eine Konstante R + Ro, anstelle von nur R, in seiner obigen Gleichung vernachlässigt, da er viele experimentelle Ergebnisse nicht besser mit Ro bschreiben konnte.

Die antagonistische logarithmische Funktion um Mittelgrau erzeugt gleiche Kontraste (gleiche Weber-Fechner-Verhältnisse) nahe Schwarz und Weiß und alle Graustufen. Durch diese Eigenschaft wird die Farbunterscheidung komplementärer Optimalfarben gleich. Die Buntheit CAB2 ist für alle komplementären Optimalfarben gleich und nicht nur für dir komplementären Ostwald-Optimalfarben.

Zum Beispiel die Unterscheidung in Helligkeitsrichtung wird durch den Quotienten dR/R bestimmt. Er ist für alle grauen Farben zwischen Schwarz N und Weiß W gleich. Zusätzlich ist er aber auch für alle Farben der Reihe zwischen Schwarz und den Ostwald-Optimalfarben und weiter bis Weiß gleich.

Betrachtet man die Normfarbwertdifferenzen deltaY für die Farbschwelle (JND) so nehmen diese von Schwarz nach Weiß stetig zu. Falls die Helligkeitsstufung durch die quadratische Reihe

L* = 100 (Y/100)^(1/2)

beschrieben wird, so haben 10 Helligkeitsstufen die Werte 1, 2, bis 10. Die zugehörigen Hellbezugswerte sind Y=1, 4, 9, ..., 81, 100.

Nahe Schwarz ist die Hellbezugswertdifferenz deltaY=3 und nahe Weiß deltaY=19. Diese Berechnung gilt für separate Farbmuster auf weißer Umgebung. Für aneinandergrenzende Farben gilt nach Weber-Fechner:

dY/Y = constant

Anmerkungen: Die Torger Holtsmark-Experimente wurden 1969/70 am Institut für Farbenmetrik im Physikalischen Institut der Universität Basel durchgeführt. Unter der Leitung von Karl Miescher waren die beiden Wissenschaftler Arne Valberg und Klaus Richter für Aufbau und Betrieb des Spektralen Farbintegrators mit verantwortlich. Klaus Richter war nach seiner Doktorarbeit in 1969, siehe
_DISS_1969_7397_Richter.pdf
einer der Versuchspersonen der Holtsmark-Experimente.


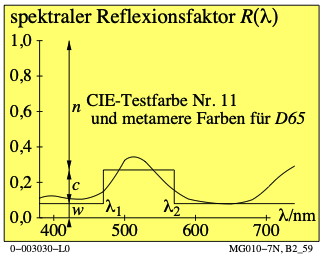
Bild 6: Spezielle metamere Farbe zur CIE-Testfarbe Nr. 11 nach CIE 13.3
Zum Herunterladen dieses Bildes in dem VG-PDF-Format, siehe MG010-7N.PDF.

Die spezielle metamere Farbe ist aus einer Ostwald-Optimalfarbe und Weiß und Schwarz gemischt. Eine Arbeit von K. Richter (1965) beschreibt die Berechnungen der vielen Optimalfarben und der besonderen metameren Farben zu vielen Körperfarben mit dem Farbintegrator.

Das Bild zeigt für eine spezielle grüne metamere Farbe den Schwarz- (n), Weiß- (w) und Buntwert (c). Der Buntwert ist definiert durch eine bunttongleiche Ostwald-Optimalfarbe mit den kompensativen Wellenlängengrenzen des Ostwald-Farbenhalbs.

Literatur:
Holtsmark, T., Valberg. A. (1969), Colour discrimination and hue, Nature 224, 366-367.
Richter, K. (1965), Programmierung farbmetrischer Berechnungen, Die Farbe 14, 275-286.
Valberg. A., Holtsmark, T., Similarity between JND-curves for complementary optimal colours (1972), in colour metrics, Institute for perception TNO, Soesterberg, 58-68.
Stiles, W. S., (1972), The line element in colour theory: A historical review, in colour metrics, Institue for perception TNO, Soesterberg, 1-25.
Richter, K. (2006), Relation of Weber law and Stevens law at achromatic threshold, see the URL (11 Seiten, 200 kB) A/BAMAT.PDF.

-------
Für Archiv-Information (2000-2009) des BAM servers "www.ps.bam.de" (2000-2018)
über Prüfvorlagen, farbmetrische Berechnungen, Normen und Veröffentlichungen, siehe
indexAE.html in englisch, indexAG.html in deutsch.

Zurück zur TUB-Hauptseite (NICHT Archiv), siehe index.html in englisch, indexDE.html. in deutsch.